【DeepSeek】一道競賽題Deepseek做出來了，Chatgpt沒解出來，有趣！

我愛數學，尤其是優美、簡潔的數學。今天給大家介紹一道不太簡單的數學競賽題，但蠻有趣的。

AI既然這麼牛，那能不能解數學競賽題呢？我得試一試。題是這樣的：

There is a polynomial P(x) with integer coefficients such that

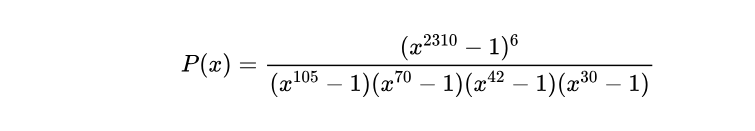
holds for every 0<x<1.Find the coefficient of x2022 in P(x).

我先用Deepseek做了一下，然後就是解答過程，AI思考了260秒，說明題目還是較難，但它的答案出乎意料居然是對的。以下是它的解答過程：

然後我用Chatgpt做了一下，很快分析得出答案，但答案是錯的。以下是它的解答過程：

結果比較有趣，後續還會嘗試更多的問題，AI真是一項偉大的發明。

真人解題過程：

分析：這道題看起來很複雜，是一個高次分式，求的是x2022前面的係數。但我們可以觀察出30、42、70和105都是2310的因子，根據公式可以對他們進行展開和化簡。

將分子拿出四次出來分別對應分母，用以下公式進行化簡：

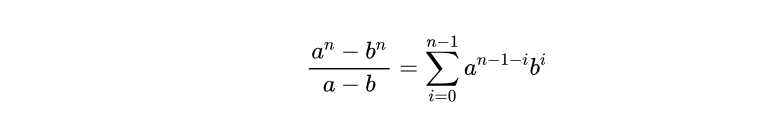
化簡後可得到以下式子成立（完整式子往左邊拉可以看到）：

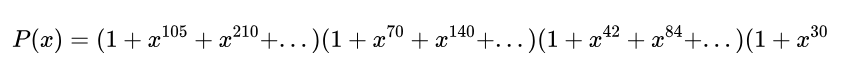
本題要求的是x2022前面的係數，所以最後一個括號只能取1，因此無須考慮。只需考慮前面四個括號的數相乘。這四個括號裡面的數相乘可以有很多種組合能出現x2022，因為每個數前面的係數都是1，所以我們只需要考慮總共有多少種可能性就可以求出x2022前面的係數，即可能性的次數就等於x2022前面的係數。

通過觀察我們可以發現第一個括號裡面x的冪次都是105的倍數，第二個括號裡面x的冪次都是70的倍數，同樣第三、四個括號裡面x的冪次分別是42和30的倍數。一次我們可以得到包含所有可能性的等式：

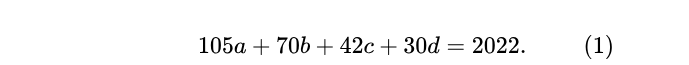
上式通過一些列的模運算可以利用球罐模型可以解決。首先將（1）式兩邊取模運算(mod2)，可得：a≡0 (mod2)，因此可得：a=2a'，代入（1）式可得：

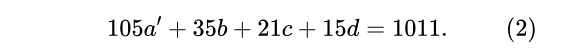
接下來將（2）式兩邊取模運算(mod3)，可得：b≡0 (mod3)，因此可得：b=3b'，代入（2）式可得：

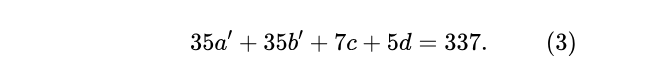
接下來將（3）式兩邊取模運算(mod5)，可得：c≡1 (mod5)，因此可得：c=5c'+1，代入（3）式可得：

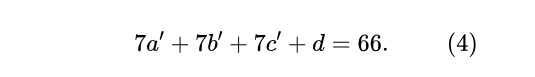
同樣的，接下來將（4）式兩邊取模運算(mod7)，可得：d≡3 (mod7)，因此可得：d=7d'+3，代入（4）式可得：

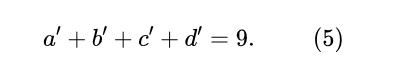
這很顯然是個球罐模型，相當於將9個球放到四個罐子裡，並且罐子可以為空，共有：

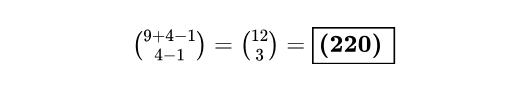
所以本題的答案為220，即x2022前面的係數為220. (ECONOMICS RULES)